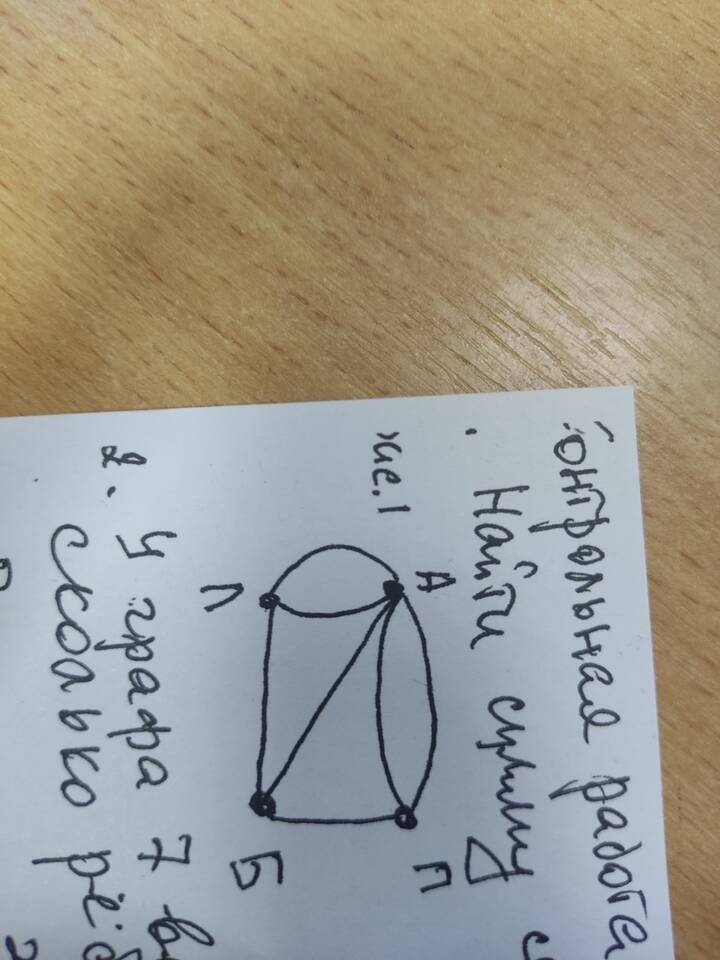
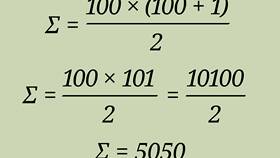В теории графов степень вершины - это количество ребер, инцидентных данной вершине. Сумма степеней всех вершин графа имеет важные теоретические и практические применения.
Содержание
Основные понятия
| Термин | Определение |
| Степень вершины | Количество ребер, связанных с вершиной |
| Петля | Ребро, соединяющее вершину саму с собой |
| Ориентированный граф | Граф с направленными ребрами |
Теорема о сумме степеней вершин
Для любого неориентированного графа сумма степеней всех вершин равна удвоенному количеству ребер:
Σdeg(v) = 2E
где deg(v) - степень вершины v, E - количество ребер в графе.
Алгоритм вычисления суммы степеней
Для неориентированного графа без петель
- Составьте список всех вершин графа
- Для каждой вершины подсчитайте количество инцидентных ребер
- Сложите степени всех вершин
- Проверьте равенство суммы удвоенному числу ребер
Для графа с петлями
- Каждая петля увеличивает степень вершины на 2
- Формула остается верной: Σdeg(v) = 2E
Пример расчета
| Вершина | Степень |
| A | 2 |
| B | 3 |
| C | 1 |
| D | 2 |
| Сумма | 8 |
Количество ребер в графе: 4
Проверка: 2 × 4 = 8
Особые случаи
Ориентированные графы
- Сумма полустепеней исхода равна сумме полустепеней захода
- Равна количеству дуг в графе
Регулярные графы
Для k-регулярного графа (все степени равны k):
Σdeg(v) = k × n
где n - количество вершин
Практическое применение
- Проверка корректности задания графа
- Анализ сетевых структур
- Решение задач теории графов
- Оптимизация компьютерных сетей
Заключение
Вычисление суммы степеней вершин - фундаментальная операция в теории графов, которая следует из леммы о рукопожатиях. Понимание этого принципа необходимо для работы с графами и решения прикладных задач в различных областях знаний.