Доверительная вероятность - это статистический показатель, отражающий вероятность того, что доверительный интервал содержит истинное значение параметра генеральной совокупности. Рассмотрим методы расчета этого важного статистического параметра.
Содержание
Основные понятия
- Доверительная вероятность (1-α) - вероятность покрытия истинного параметра
- Уровень значимости (α) - вероятность ошибки
- Доверительный интервал - диапазон значений параметра
- Критическое значение - граничное значение распределения
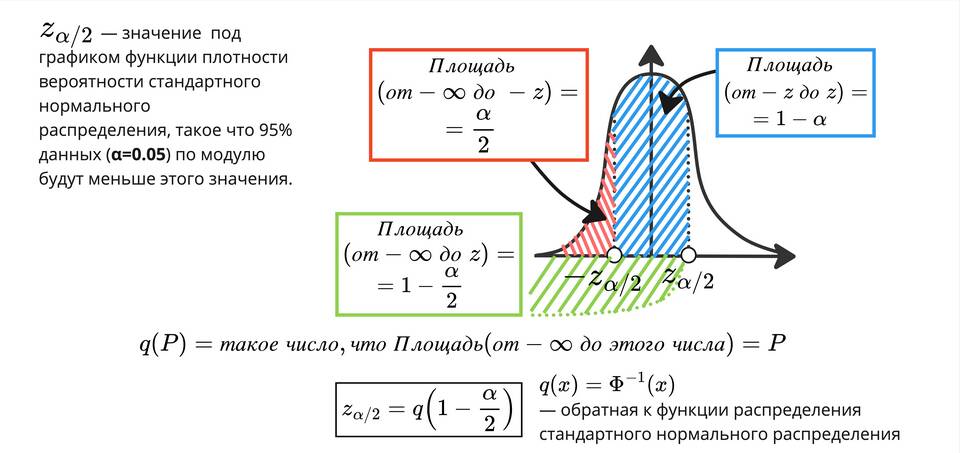
Формула расчета доверительной вероятности
P(θ ∈ [L,U]) = 1 - α
где θ - оцениваемый параметр, [L,U] - границы доверительного интервала
Пошаговый алгоритм расчета
Определение параметров распределения
- Выберите уровень значимости α (обычно 0.05 или 0.01)
- Определите объем выборки n
- Вычислите выборочное среднее и стандартное отклонение
Выбор статистического распределения
| Условие | Используемое распределение |
| n > 30 или известно σ | Нормальное (z-распределение) |
| n ≤ 30 и σ неизвестно | t-распределение Стьюдента |
Пример расчета для среднего значения
- Задайте доверительную вероятность (например, 95%)
- Найдите критическое значение zα/2 (для 95% это 1.96)
- Вычислите стандартную ошибку: SE = σ/√n
- Определите границы интервала: x̄ ± zα/2 × SE
Факторы, влияющие на доверительную вероятность
| Фактор | Влияние на доверительную вероятность |
| Объем выборки | Увеличение n уменьшает ширину интервала |
| Разброс данных | Большее σ увеличивает ширину интервала |
| Уровень доверия | Более высокий уровень → шире интервал |
Типовые значения доверительной вероятности
- 90% (α = 0.10) - z = 1.645
- 95% (α = 0.05) - z = 1.960
- 99% (α = 0.01) - z = 2.576
Практическое применение
В научных исследованиях
- Определение необходимого объема выборки
- Оценка точности измерений
- Проверка статистических гипотез
В бизнес-аналитике
- Прогнозирование продаж
- Оценка доли рынка
- Анализ эффективности маркетинговых кампаний
Программные средства для расчета
| Программа | Функция расчета |
| Excel | ДОВЕРИТ.НОРМ() / CONFIDENCE.NORM() |
| R | qnorm(), qt() |
| Python | scipy.stats.norm.ppf(), t.ppf() |
Расчет доверительной вероятности требует понимания основных статистических принципов и внимательного подхода к выбору методов анализа. Правильное определение доверительных интервалов позволяет делать обоснованные выводы на основе выборочных данных.