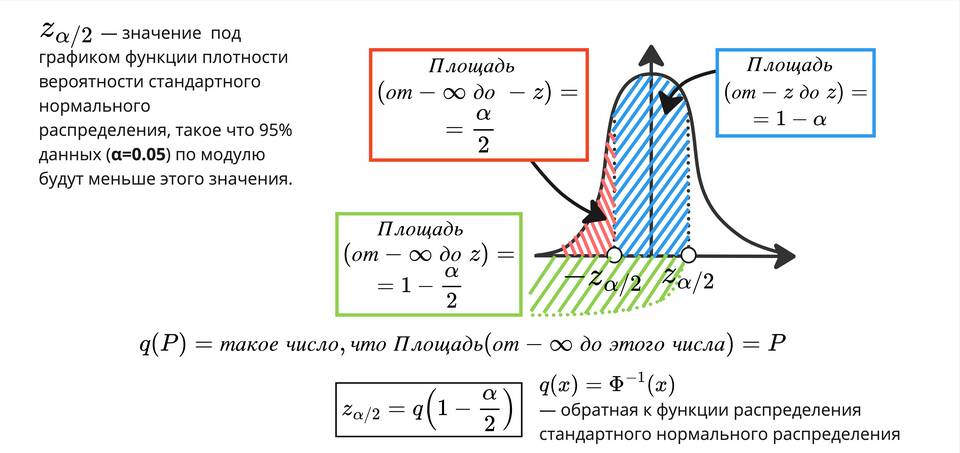
Доверительный интервал представляет собой диапазон значений, который с определенной вероятностью содержит истинное значение оцениваемого параметра. Рассмотрим методы построения доверительных интервалов для различных типов данных.
Содержание
- Основные понятия
- Пошаговый алгоритм построения
- Критические значения для разных уровней доверия
- Особые случаи
- Малые выборки (nИспользуйте t-распределение СтьюдентаУчитывайте степени свободы (n-1)Формула: x̄ ± t*(s/√n)Разность среднихВычислите разность выборочных средних (x̄₁ - x̄₂)Определите объединенную стандартную ошибкуИспользуйте соответствующее распределениеПостройте интервал для разностиПрактические рекомендацииДля нормально распределенных данных используйте z-интервалПри неизвестном σ и малых выборках применяйте t-интервалДля пропорций используйте нормальное приближение при np>5 и n(1-p)>5При нарушении условий рассмотрите точные методы или бутстрепИнтерпретация результатов
- Разность средних
- Практические рекомендации
- Интерпретация результатов
Основные понятия
- Доверительная вероятность - вероятность того, что интервал содержит истинное значение параметра (обычно 90%, 95% или 99%)
- Точечная оценка - выборочное значение оцениваемого параметра
- Предельная ошибка - половина ширины доверительного интервала
Пошаговый алгоритм построения
Для среднего значения (нормальное распределение)
- Вычислите выборочное среднее (x̄)
- Определите стандартное отклонение (σ) или стандартную ошибку (SE)
- Выберите уровень доверия (1-α)
- Найдите критическое значение z* для нормального распределения
- Рассчитайте интервал: x̄ ± z*(σ/√n)
Для доли признака
- Вычислите выборочную долю (p̂)
- Определите стандартную ошибку: SE = √[p̂(1-p̂)/n]
- Используйте z-распределение для больших выборок (n>30)
- Формула интервала: p̂ ± z*SE
Критические значения для разных уровней доверия
| Доверительная вероятность | z-критерий (норм. распределение) | t-критерий (n=30) |
| 90% | 1.645 | 1.697 |
| 95% | 1.960 | 2.042 |
| 99% | 2.576 | 2.750 |
Особые случаи
Малые выборки (n<30)
- Используйте t-распределение Стьюдента
- Учитывайте степени свободы (n-1)
- Формула: x̄ ± t*(s/√n)
Разность средних
- Вычислите разность выборочных средних (x̄₁ - x̄₂)
- Определите объединенную стандартную ошибку
- Используйте соответствующее распределение
- Постройте интервал для разности
Практические рекомендации
- Для нормально распределенных данных используйте z-интервал
- При неизвестном σ и малых выборках применяйте t-интервал
- Для пропорций используйте нормальное приближение при np>5 и n(1-p)>5
- При нарушении условий рассмотрите точные методы или бутстреп
Интерпретация результатов
Доверительный интервал 95% для среднего дохода [45 000; 55 000] означает, что если бы мы многократно повторяли выборку, в 95% случаев построенные интервалы содержали бы истинное среднее значение дохода в генеральной совокупности.
Правильно построенный доверительный интервал позволяет оценить точность точечной оценки и учитывает вариабельность данных, что делает его важным инструментом статистического анализа.